I am currently a Master student in Computational Science and Engineering at Technische Universität München (TUM). Before, I had a Bachelor Degree in Physics at National Taiwan University.
Contact: shenghsuan.lastname@tum.de
Research Interest
My research interest is in the numerical methods in Condensed Matter Physics (CMT) and Machine Learning (ML).
Tensor network methods provide efficient representations and operations on the high dimensional tensors in physics. These methods are also known as the tensor decomposition methods in applied math community. They, especially EPS/CPS, are connected and related with probabilistic graphical models (PGM) in machine learning. Various machine learning algorithms are also related to low dimension representation of high dimension problems. These connection brings forward many promising application of numerical methods from CMT to ML and vise versa.
Projects
Solving the Quantum Many-Body Problem with Feedforward Neural Networks
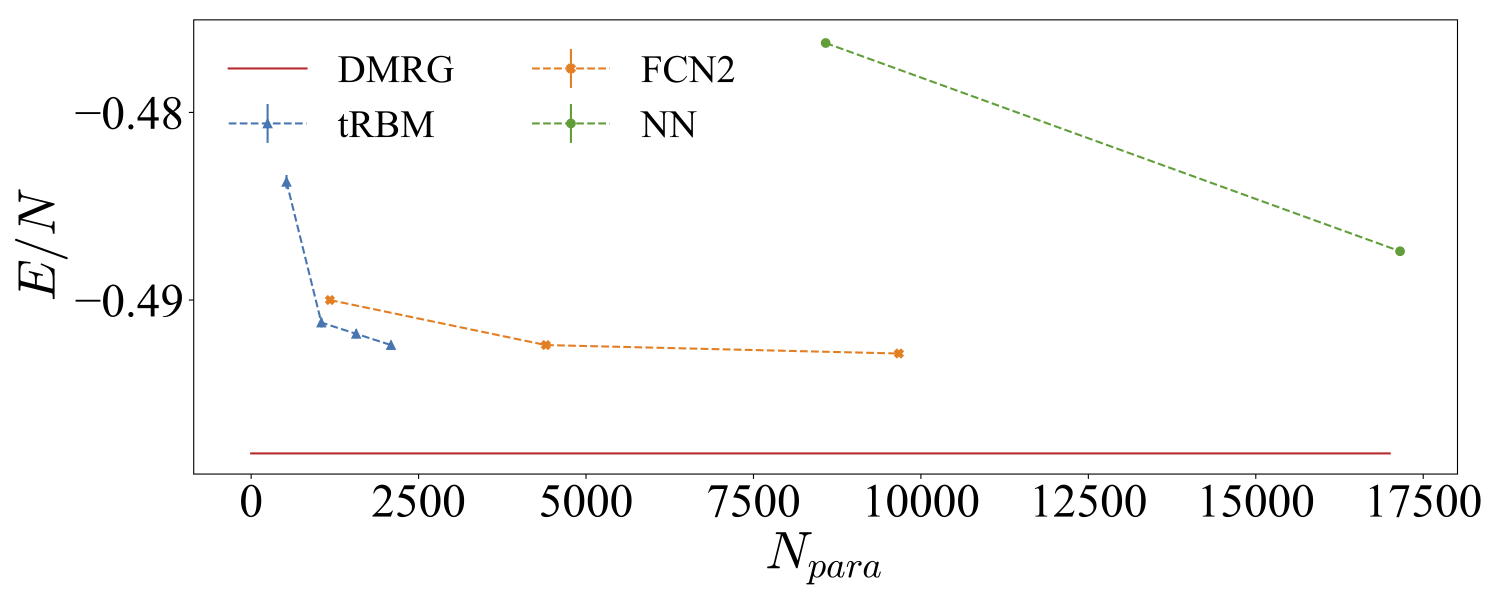
Motivated by the success of describing quantum states with restricted Boltzmann machine, we consider general feed-forward neural networks as variational wavefunctions. We show that with variational Monte Carlo method or with supervised learning, neural networks could be trained to represent quantum states. We demonstrated the ability of neural network representing quantum states on frustrated problems including 1d and 2d J1-J2 model. The difficulties of optimization large number of parameters are addressed. Considering the connection between natural gradient method and stochastic reconfiguration method, we point out possible way to extend the result to deep networks with large number of parameters.
Thesis pdf here.
The project repository is currently held private. Contact me if interested.
(Tensorized) Residual Network
A self implemented residual network, serving as a backbone network for other projects.
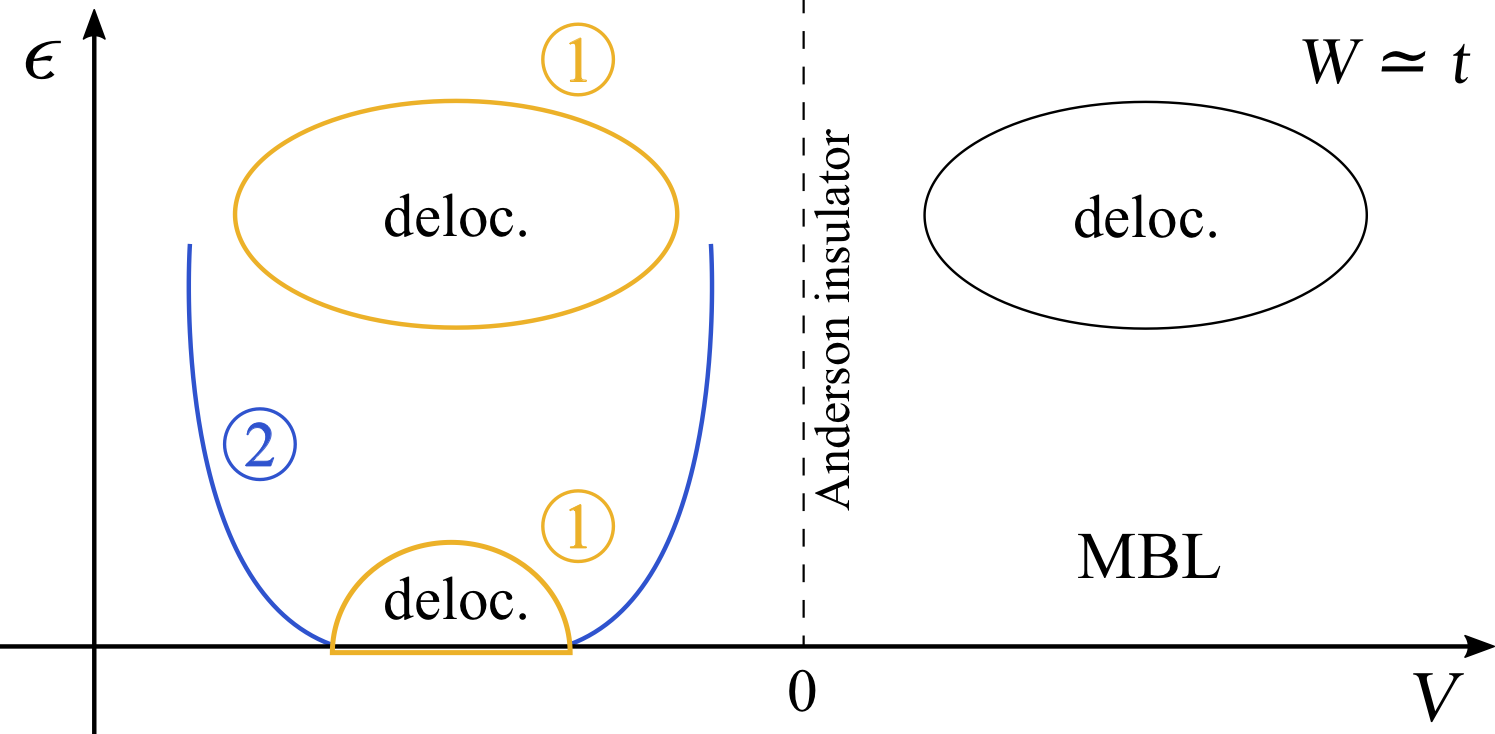
Many-body localization of spinless fermions with attractive interactions in one dimension
![](img src="./figures/cases.png" alt="please let me know if the figures are not displayed on the website." width="200"){kind=link}
We study the finite-energy density phase diagram of spinless fermions with attractive interactions in one dimension in the presence of uncorrelated diagonal disorder. Unlike the case of repulsive interactions, a delocalized Luttinger-liquid phase persists at weak disorder in the ground state, which is a well-known result. We revisit the ground-state phase diagram and show that the recently introduced occupation-spectrum discontinuity computed from the eigenspectrum of one-particle density matrices is noticeably smaller in the Luttinger liquid compared to the localized regions. Moreover, we use the functional renormalization scheme to study the finite-size dependence of the conductance, which resolves the existence of the Luttinger liquid as well and is computationally cheap. Our main results concern the finite-energy density case. Using exact diagonalization and by computing various established measures of the many-body localization-delocalization transition, we argue that the zero-temperature Luttinger liquid smoothly evolves into a finite-energy density ergodic phase without any intermediate phase transition. As a consequence, the full energy-density versus interaction strength diagram has a pronounced asymmetry between the attractive and the repulsive side.
More detail, see SciPost Phys. 4, 002
Code
Ongoing Projects
Tensorizing Residual Network
Tensorizing Residual Network with Tensor Train (TT) decomposition. There are three directions to explore. 1. compression of ResNet 2. Tensor Train as regularization 3. Wider ResNet
Tensor Network Toolbox
This is a very rough self implemented routine for some matrix product state (MPS) / tensor train (TT) functions.
Comments and discussion are welcome.